1. Единица в углу
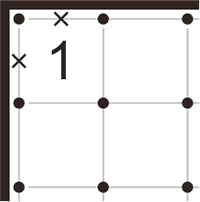
Если единица находится в углу, обе линии этого угла могут быть зачеркнуты (потому что линия, входящая в эту ячейку, не может ее покинуть, не пройдя вторично возле цифры “1”).
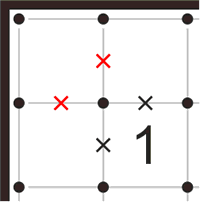
Этот метод также применим в том случае, когда две линии, входящие в ячейку с цифрой “1” в том же самом углу, являются зачеркнутыми.
2. Две тройки рядом
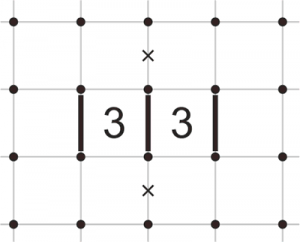
Если две тройки находятся рядом по горизонтали или вертикали, между ними должна быть нарисована линия. Также должны быть нарисованы две внешних линии группы (параллельные общей для обеих троек линии). И наконец — линия, проходящая через две расположенные рядом тройки, всегда будет «обертываться» вокруг них в форме буквы “S”. Поэтому линия между двумя тройками не может продолжаться по прямой. Вычеркиваем соответствующие стороны и получаем конечный результат.
3. Две тройки по диагонали
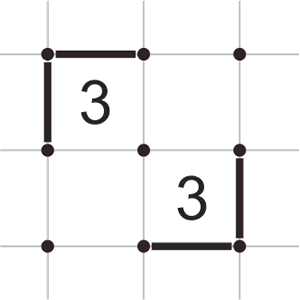
Если две тройки расположены рядом по диагонали, в краях, которые не сталкиваются с общей для обеих троек точкой, должны быть нарисованы линии.
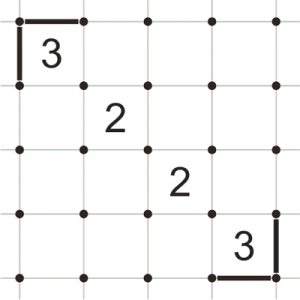
Если две тройки находятся на одной диагонали, но отделены парой (или несколькими парами) двоек, во внешних краях этих троек также должны быть нарисованы линии, как если бы они были расположены рядом по диагонали.
4. Тройка рядом с линией
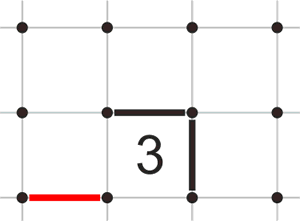
Если линия подходит к углу ячейки с тройкой, должны быть нарисованы линии с обеих сторон тройки у противоположного угла.
5. Двойка рядом с линией
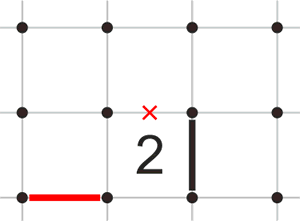
Если линия подходит к углу ячейки с двойкой, а одна из сторон ячейки (выходящая из противоположного угла) вычеркнута, то в другой стороне, выходящей из противоположного угла, должна быть нарисована линия.
6. Единица рядом с линией
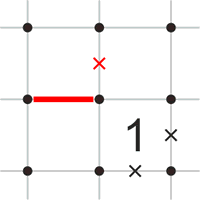
Если линия подходит к углу ячейки с единицей, а один из трех вариантов продолжения линии (не входящий в ячейку с единицей) вычеркнут, то две стороны противоположного угла должны быть вычеркнуты.
В исключительно трудных головоломках можно использовать следующую математическую теорему: “Любая открытая кривая, которая начинается и заканчивается за пределами закрытой кривой, должна пересечь закрытую кривую четное число раз”.
В частности это означает, что любую строку и любой столбец головоломки должно пересекать четное число вертикальных или горизонтальных линий соответственно. Когда только один потенциальный сегмент в строке или столбце неизвестен, с помощью этой теоремы вы можете определить, является ли этот сегмент частью петли или нет.