1. Переполнение
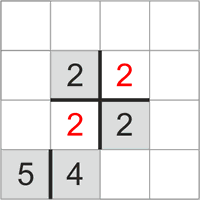
Если существует ячейка, добавление определенного числа в которую привело бы к ошибке, то есть “переполнению” числами блока, значит, она должна принадлежать к другому блоку.
Как следствие — расположенные по диагонали двойки должны обязательно принадлежать к разным блокам.
2. Ограничение
Каждое число в сетке, заданное или введенное, в конечном итоге должно “расшириться” в блок. Часто бывает, что возможности для подобного «расширения» ограничены.
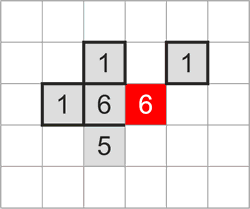
Самый очевидный случай — любое (кроме единицы) число ограничено с трех сторон по горизонтали и вертикали другими числами. Ячейка с последней, четвертой стороны должна принадлежать тому же блоку.
2.1 Так, на рисунке число “6” ограничено с трех сторон другими числами и может “расширяться” только вправо (выделено красным).
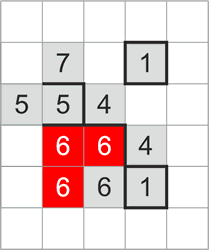
2.2 Тот же принцип применим и к числам, ограниченным с двух сторон, но не имеющих достаточного количества свободных соседних ячеек для расширения.
3. Пустые ячейки
Часто при неопределнностях, возникающих в процессе решения филломино, проще “работать” с пустыми ячейками, чем с числами.
3.1. Самый очевидный случай — когда единственная ячейка без числа “окружена” со всех сторон числами, уже сформировавшими блоки. Единственный вариант числа для такой ячейки — “1”.
3.2. Точно так же две расположенные ортогонально (по горизонтали или по вертикали) ячейки, окруженные со всех сторон числами, уже сформировавшими блоки, могут содержать только число “2”.
3.3. Также ячейки в областях, не полностью окруженных другими числами, могут быть определены.
Обычным явлением для пустой ячейки, являющейся соответственно частью небольшой пустой области, главным образом ограниченной решенными блоками, есть наличие только одного возможного размера блока. Другие размеры либо слишком велики для области, либо нарушают правило, запрещающее ортогональное соприкосновение блоков одинакового размера.