Понимание того, как круги “взаимодействуют” друг с другом, является ключом к решению головоломки. Поиск решения нужно начинать от края сетки.
1. Любой сегмент линии, выходящий из черного круга, должен пройти две ячейки без смены направления, не пересекая при этом другой сегмент или внешнюю границу. У каждой ячейки с черным кругом должно быть два таких сегмента, расположенные под прямым углом. Значит, если сегмент линии не может пройти через черный круг в одном направлении, он должен обязательно пройти в противоположном .
Например, если нет возможности провести сегмент линии через две ячейки из черного круга вверх, то линия должна обязательно пройти две ячейки вниз. Из вышесказанного следует:
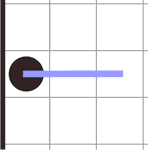
а) у любого черного круга, расположенного вдоль внешней границы головоломки или на расстоянии одной ячейки нее, должен быть сегмент, уводящий от границы, т.е. перпендикулярный к ней;
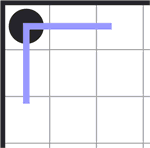
б) соответственно, для черного круга, расположенного в углу головоломки, существует единственный способ провести через него линию;
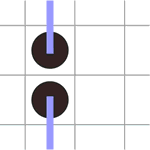
в) у двух черных кругов, расположенных в соседних (не диагональных) ячейках, должны быть сегменты, выходящие из них в противоположных направлениях.
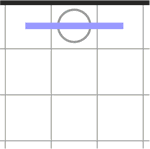
2. Через любой белый круг, расположенный рядом с границей головоломки, обязательно должен пройти сегмент линии, параллельный границе.
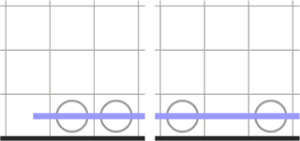
3. Если два белых круга расположены вдоль границы в соседних ячейках (или разделенные одной ячейкой), сегмент линии должен пройти через них параллельно границе, не поворачивая при этом.
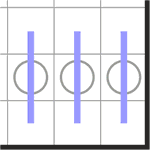
4. Если три или больше белых круга будут расположены в соседних (не диагональных) ячейках вдоль одной линии, то сегмент должен будет пройти через каждый круг перпендикулярно к линии, вдоль которой расположены круги.
5. Невозможность “коротких замыканий”: поскольку решением головоломки является единственная замкнутая линия, любой сегмент, который замкнул бы эту линию, не прошедшую через все круги, запрещен.